particles version 0.4: single-run variance estimates, FFBS variants, nested sampling

news
particles
SMC
Author

Nicolas Chopin

Published

September 1, 2023

Modified

September 6, 2023

Version 0.4 of particles have just been released. Here are the main changes:

Single-run variance estimation for waste-free SMC

Waste-free SMC (Dau & Chopin, 2020) was already implemented in particles (since version 0.3), and even proposed by default. This is a variant of SMC samplers where you resample only \(M \ll N\) particles, apply to each resampled particle \(P-1\) MCMC steps, and then gather these \(M\times P\) states to form the next particle sample; see the paper if you want to know why this is a good idea (short version: this tends to perform better than standard SMC samplers, and to be more robust to the choice of the number of MCMC steps).

What was not yet implemented (but is, in this version) is the single-run variance estimates proposed in the same paper. Here is a simple illustration:

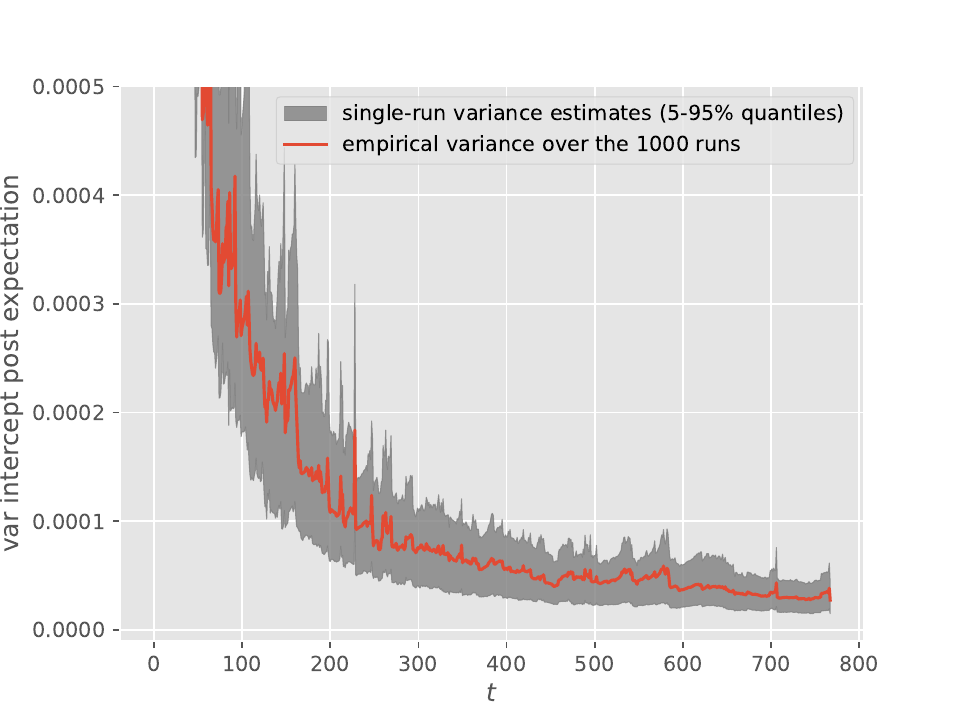
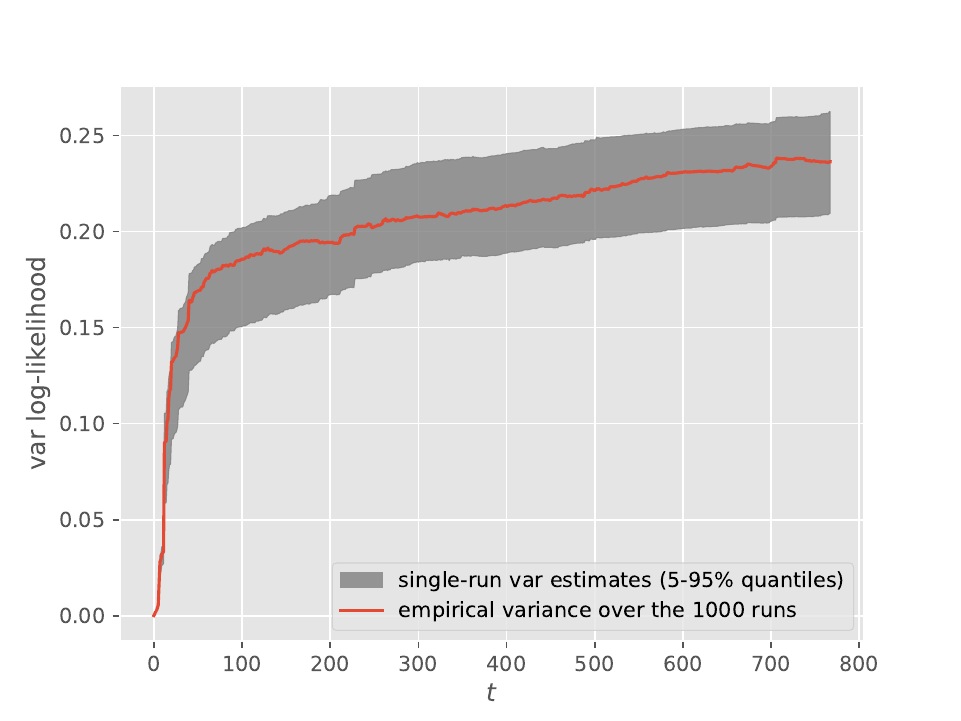
Both plots were obtained from \(10^3\) runs of waste-free IBIS (i.e. target at time \(t\) is the posterior based on the first \(t+1\) observations, \(p(\theta|y_{0:t})\)) applied to Bayesian logistic regression and the Pima Indians dataset. The red line is the empirical variance of the output, and, since the number of runs is large, it should be close to the true variance. The lower (resp. upper) limit of the grey area is the \(5\%\) (resp. \(95\%\)) quantile of the single-run variance estimates obtained from these \(10^3\) runs. The considered output is either the posterior mean of the intercept (top) or the log marginal likelihood (bottom).

We can see from these plots that these single-run estimates are quite reliable, and make it possible, in case one uses IBIS, to obtain error bars even from a single run. See the documentation of module smc_samplers (or the scripts in papers/wastefreeSMC) for more details on how you may get such estimates.

New FFBS variants

I have already mentioned in a previous post, on the old blog, that particles now implement new FFBS algorithms (i.e. particle smoothing algorithms that rely on a backward step) that were proposed in this paper. On top of that, particles now also includes a hybrid version of the Paris algorithm.

Nested sampling

I was invited to this nested sampling workshop in Munich, so this gave me some incentive to:

  • clean up and document the “vanilla” nested sampling implementation which was in module nested.

  • add to the same module the NS-SMC samplers of Salomone et al (2018) to play with them and do some numerical experiments to illustrate my talk.

I will blog shortly about the interesting results I found (which essentially are in line with Salmone et al).

Other minor changes

Several distributions and a dataset (Liver) were added, see the change log.

What’s next?

I guess what’s still missing from the package are stuff like:

  • the ensemble Kalman filter, which would be reasonably easy to add, and would be useful in various problems;

  • advanced methods to design better proposals, such as controlled SMC (Heng et al, 2020) or the iterated auxiliary particle filter (Guarniero et al, 2017).

If you have other ideas, let me know.

Feedback

I have not yet looked into how to enable comments on a quarto blog. You can comment by replying to this post on Mastodon, or to the same post on LinkedIn (coming soon); or you can raise an issue on github or send me an e-mail, of course.